Construtivismo no ensino de Matemática: funciona?

O ensino construtivista de matemática é uma abordagem inovadora que pode ajudar as crianças a aprenderem de forma mais eficaz, e ainda pode ser utilizada como alternativa para sanar dificuldades de aprendizagem apresentadas pelas crianças.
Neste artigo, você vai conhecer o construtivismo no ensino de matemática infantil e descobrir como aplicar essa corrente pedagógica na prática.

Corrente pedagógica construtivista para ensinar crianças: matemática concreta com jogos manipulativos
Primeiramente, neste guia, você vai entender por que o construtivismo no ensino de matemática infantil funciona tão bem. Primeiramente, conhecerá os princípios do construtivismo para crianças pequenas. Em seguida, aprenderá a usar materiais manipulativos e jogos pedagógicos para tornar conceitos abstratos visíveis. Além disso, verá como montar rotinas e promover aprendizagem ativa em sala. Igualmente, saberá favorecer a interação social e apoiar o avanço pela Zona de Desenvolvimento Proximal (ZDP) sem tirar o desafio. Por fim, aprenderá a observar o processo com avaliação formativa e a planejar atividades práticas que geram aprendizagem significativa.
Principais aprendizados
- Primeiramente, você aprende fazendo e experimentando.
- Em segundo lugar, seu pensamento cresce com problemas reais.
- Em terceiro lugar, você constrói conceitos com materiais concretos.
- Além disso, seus erros viram aprendizado.
- Por fim, você trabalha em grupo e troca ideias.
Descubra o construtivismo no ensino de matemática infantil: estratégias, jogos manipulativos, avaliação formativa e rotinas para professores em creches, escolas e abrigos. Guia prático para aprendizagem ativa e significativa.

O que é a corrente pedagógica construtivista e por que funciona na matemática
Essencialmente, o construtivismo no ensino de matemática infantil baseia-se na ideia de que as crianças constroem ativamente o conhecimento a partir de experiências, interações e resolução de problemas. Nesse sentido, a corrente defendo que em vez de receberem informações prontas, os alunos aprendem melhor quando manipulam objetos concretos, exploram padrões e formulam explicações próprias. Consequentemente, a aprendizagem torna-se mais profunda e duradoura. Para uma revisão teórica veja Princípios do construtivismo em educação.
- Primeiramente, construção do conhecimento: fundamentalmente, a criança interpreta e reorganiza suas ideias anteriores. Além disso, o professor atua como mediador, propondo desafios e registrando progressos.
- Em segundo lugar, por que funciona no construtivismo no ensino de matemática infantil: essencialmente, a matemática é abstrata. Dessa forma, o construtivismo oferece uma ponte concreta por meio de materiais manipulativos. Consequentemente, a prática ativa e o erro produtivo favorecem a generalização de conceitos, alinhando-se a evidências de neurociência na educação.
- Finalmente, aplicabilidade: em creches prioriza-se exploração sensorial e noção de quantidade. Por outro lado, em escolas e abrigos trabalha-se resolução de problemas, argumentação e comunicação matemática, considerando o desenvolvimento infantil na escola.
“Aprender matemática não é memorizar passos, mas construir sentidos.”
De fato, esta frase sintetiza o espírito do construtivismo: essencialmente, compreensão antes de procedimentos.
Princípios do construtivismo no ensino de matemática infantil para crianças pequenas
A seguir, os princípios guiam práticas que respeitam o desenvolvimento infantil e promovem matemática significativa no construtivismo no ensino de matemática infantil.
- Em primeiro lugar, aprendizagem ativa e intencional: nesse contexto, crianças aprendem fazendo, explorando e explicando. Paralelamente, professores planejam situações com propósito matemático.
- Em segundo lugar, papel central do erro: especificamente, o erro revela concepções e possibilita ajustamentos. Por isso, incentive reflexões: por que deu errado? Dessa forma, o que podemos tentar diferente? (prática apoiada por estratégias pedagógicas baseadas em neurociência).
- Em terceiro lugar, contextualização e significado: fundamentalmente, problemas relacionados ao cotidiano tornam a matemática relevante. Portanto, use histórias, brincadeiras e desafios reais.
- Progressão dos conceitos — do concreto para o pictórico e depois para o simbólico; reapresente conceitos em contextos variados, valorizando a aprendizagem significativa na educação infantil.
- Interação social — o diálogo é ferramenta de construção coletiva de conceitos; aprendizagens emergem em trocas mediadas pelo professor.
- Zoneamento e diferenciação — trabalhar dentro da Zona de Desenvolvimento Proximal (ZDP) para promover avanços; ajustar apoio: modelagem, pistas, perguntas orientadoras.
Consulte também as Diretrizes da BNCC para educação infantil para alinhar objetivos e competências em suas propostas pedagógicas.
Corrente pedagógica construtivista para ensinar crianças matemática concreta com jogos manipulativos na sala de aula
Fundamentalmente, ensinar matemática concreta com jogos manipulativos significa organizar atividades onde os alunos experimentam, testam hipóteses e discutem resultados. A seguir, orientações práticas mantendo o foco na corrente pedagógica construtivista para ensinar crianças matemática concreta com jogos manipulativos na sala de aula. Para aplicar o construtivismo no ensino de matemática:
Primeiramente, planejamento de jogos:
- Inicialmente, defina o objetivo matemático claro (ex.: compreender pares, ordinalidade, adição básica).
- Em seguida, escolha materiais manipulativos acessíveis (botões, cubos, tampas) e recursos de apoio para professores e cuidadores (apoio a educadores que cuidam de crianças).
- Por fim, estabeleça regras simples e adaptáveis
Estrutura de uma sessão manipulativa
- Apresentação do desafio com pergunta focada.
- Tempo livre para exploração individual e em pares.
- Partilha de estratégias e conclusões em grande grupo.
Papéis do professor
- Observador ativo: registra estratégias e dificuldades.
- Mediador: faz perguntas abertas, sugere variações e amplia representações.
- Avaliador formativo: anota evidências de compreensão. Profissionais podem se apoiar em processos de formação continuada de professores para ampliar práticas de mediação e avaliação.
Exemplo prático:
Jogo das oito colheres
- Objetivo: contar, comparar e agrupar.
- Materiais: 16 colheres coloridas, dois recipientes.
- Descrição: cada criança coloca colheres em recipientes conforme o sorteio (cada criança aponta com os dedos um número, depois compara quantidades e registra com desenhos.
- Variações: aumente a complexidade mudando o número de objetos; introduza perguntas para promover generalização: “O que acontece se…?”
Leia: Estratégias pedagógicas baseadas em neurociência na escola.
Benefícios da aprendizagem ativa em matemática na educação infantil – construtivismo no ensino de matemática
A aprendizagem ativa traz múltiplos benefícios cognitivos, afetivos e sociais para crianças pequenas.
- Desenvolvimento cognitvo: melhora a compreensão conceitual e a habilidade de resolver problemas; favorece transferências entre contextos distintos e envolve habilidades como memória de trabalho e atenção, ligadas ao desenvolvimento das funções executivas.
- Engajamento e motivação: atividades lúdicas aumentam interesse e persistência; crianças se sentem capazes ao construir respostas próprias.
- Dessa forma, habilidades sociais e comunicativas: consequentemente, trabalho em pares e grupos desenvolve linguagem matemática e argumentação, conectando-se a competências socioemocionais (competências socioemocionais na escola) e a importância dos vínculos afetivos e aprendizagem.
- Além disso, inclusão e diferenciação: especificamente, materiais concretos permitem múltiplas vias de acesso ao conteúdo. Portanto, adaptam-se ritmos e estilos de aprendizagem com base em práticas inclusivas e atenção a necessidades especiais.
- Finalmente, retenção e automatização: efetivamente, conceitos bem construídos são lembrados por mais tempo e aplicados com flexibilidade.
| Benefício principal | Exemplos práticos | Evidência observável |
|---|---|---|
| Compreensão conceitual | Uso de blocos para operações básicas | Explicações próprias das crianças |
| Motivação | Jogos e desafios curtos | Maior tempo de atenção |
| Comunicação | Discussões sobre estratégias | Uso de vocabulário matemático |
| Inclusão | Variação de materiais | Participação de todos os alunos |
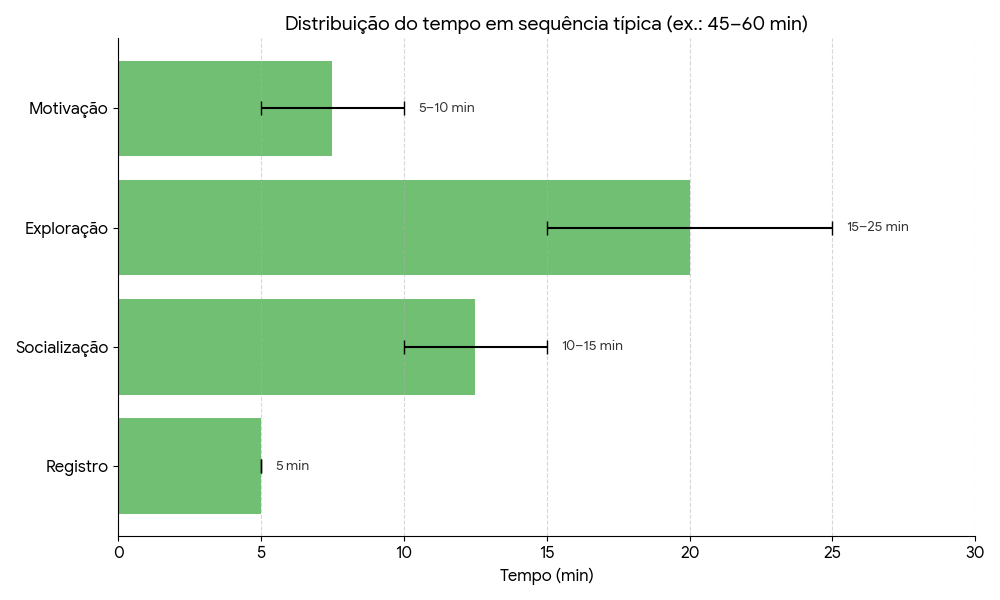
Distribuição do tempo em sequência típica (ex.: 45–60 min)
Materiais manipulativos para matemática: escolhas simples e eficazes – ensino construtivista
Sem sombra de dúvida, escolher materiais simples, reutilizáveis e multifuncionais é fundamental. Assim, para orientações internacionais sobre uso prático, consulte Uso de materiais manipulativos na matemática. Abaixo, lista organizada por objetivos.
- Noção de quantidade e contagem: tampinhas, botões, feijões; recipientes transparentes.
- Operações e agrupamentos: cubos de encaixe, blocos de montar, ábacos; fitas adesivas para criar “casas”.
- Forma e medida: blocos geométricos, dobraduras, fitas métricas simples; bandejas e colheres para estimativas.
- Padrões e relações: contas coloridas, cartões de padrão, instrumentos sonoros para ritmo.
- Materiais de baixo custo: caixas, palitos, elásticos; cartões com números e imagens. Recursos práticos e ideias de baixo custo podem ser consultados em materiais de apoio a educadores (apoio a educadores que cuidam de crianças).
Tabela comparativa de materiais
| Material | Objetivos principais | Vantagem prática |
|---|---|---|
| Tampinhas | Contagem, agrupamento | Barato e disponível |
| Cubos de encaixe | Operações, construção | Visual e modular |
| Cartões numéricos | Reconhecimento, correspondência | Portátil e organizado |
| Fitas coloridas | Organização espacial, medidas | Fácil de ajustar |
| Blocos geométricos | Forma e proporção | Estímulo visual e tátil |
Como aplicar ensino por descoberta e promover resolução de problemas na infância
Essencialmente, o ensino construtivista por descoberta deve ser planejado com intencionalidade para que as crianças possam explorar, formular hipóteses e chegar a conclusões.
- Inicialmente, entenda os Elementos principais: problema autêntico, material e tempo suficientes, perguntas norteadoras (não respostas prontas).
- Seguidamente, atente-se em relação à mediação docente: especialmente, faça perguntas abertas, peça justificativas e sugira variações. Além disso, estratégias aqui descritas se beneficiam de estudos sobre aprendizagem significativa e de estratégias baseadas em neurociência.
- Quanto à sequência: inicialmente, apresentação do desafio. Em seguida, exploração livre com registro (desenhos, marcações). Posteriormente, socialização de estratégias. Por fim, sistematização e generalização pelo professor.
- Por Exemplo: “Lojinha das frutas” — vender e trocar frutas usando contadores, inferir operação (adição/subtração); reflexão final com escrita simbólica e verbalização.
- Avaliação na descoberta: registre estratégias, perguntas e mudanças de raciocínio para planejar intervenções futuras, incluindo atenção a sinais de dificuldades de aprendizagem quando necessário.
Exemplos práticos para usar já: Jogos matemáticos pedagógicos
Jogos testados em educação infantil, com objetivo, materiais e passo a passo.
- Loja dos Trocos — compreensão de troca e valor. Materiais: objetos com etiquetas 1–5, moedas simbólicas.
- Padrões em Cadeia — reconhecer e continuar padrões. Materiais: contas coloridas, cartões.
- Caça ao Par — correspondência e paridade. Materiais: cartões com imagens e números/quantidades.
- Construindo Pontes (cooperativo) — medidas e comparação. Materiais: blocos, réguas; construir em equipes e medir.
Jogos também podem ser adaptados para crianças com necessidades específicas e para intervenções mais individualizadas (veja orientações sobre inclusão escolar e necessidades especiais e https://pedagogiando.space/praticas-inclusivas-na-educacao-basica
Estratégias para garantir aprendizagem significativa matemática com atividades concretas para o ensino construtivista.
Inicialmente, algumas estratégias docentes são essenciais para transformar experiências em aprendizagem significativa.
- Definir objetivos claros e observáveis.
- Variar representações: objetos concretos, desenhos, linguagem e símbolos.
- Promover metacognição: incentive explicações do processo e práticas de autorregulação emocional que ajudam a criança a monitorar seu raciocínio.
- Repetição com variação para generalização.
- Uso sistemático de registros: amostras de trabalho, fotos e notas.
- Feedback descritivo e específico.
- Diferenciação com base em evidências: oferecer desafios ou suporte conforme desempenho, com atenção a possíveis dificuldades de aprendizagem.
Formação contínua e troca entre professores fortalecem essas práticas (formação continuada de professores).
Abordagem construtivista na educação infantil: rotinas e organização da sala
Desta forma, a organização física e as rotinas influenciam diretamente o trabalho do construtivismo no ensino de matemática.
- Ambientes por centros de aprendizagem: canto de manipulação, contação de histórias, medidas e construção.
- Materiais organizados em caixas rotuladas e acessíveis.
- Rotinas: início da aula com desafio breve, tempo livre para exploração seguido de socialização.
- Gestão do tempo: sessões curtas e variadas; planeje momentos de registro e reflexão. (Veja práticas de gestão de sala de aula para organizar espaços e rotinas.)
- Materiais de apoio: kits prontos, fichas de observação e rubricas simples.
- Criação de cultura de investigação: exponha perguntas em mural; valorize tentativa, erro e reformulação.
Interação social e aprendizagem matemática: trabalho em pares e em grupo
Desse modo, aprender com colegas amplia estratégias cognitivas e desenvolve linguagem matemática.
- Quanto aos formatos: inicialmente, pares para troca de estratégias; em seguida, pequenos grupos para problemas complexos; por fim, grande grupo para socialização.
- Em relação aos benefícios: primeiramente, ampliação de repertório, desenvolvimento de argumentação e defesa de ideias. Assim, essas habilidades dialogam com o desenvolvimento de competências socioemocionais e com a construção de vínculos afetivos na escola.
- Quanto ao papel do professor: essencialmente, formular tarefas que exijam colaboração, observar interações e intervir quando necessário.
- Em relação às dicas práticas: primeiramente, defina papéis (contador, registrador, conferidor) e troque-os. Além disso, use cartões de ajuda com perguntas-guia.
- Por fim, avaliação: consequentemente, rubricas simples (participação, uso de estratégias, capacidade de explicar) e registro de contribuições individuais.
Zona de desenvolvimento proximal: como apoiar o avanço sem resolver por completo
A ZDP orienta como oferecer suporte que promova autonomia. Leia mais sobre o Conceito de ZDP e mediação docente.
- Identificação: observe o que a criança consegue sozinha e com ajuda.
- Tipos de suporte (scaffolding): modelagem, pistas, simplificação em etapas menores; esses recursos dialogam com o desenvolvimento das funções executivas e com estratégias profissionais (veja desenvolvimento das funções executivas).
- Evitar resolver por completo: faça perguntas que estimulem a reflexão; demonstre uma parte e peça que a criança complete.
- Escalonamento do apoio: diminua gradualmente o suporte; reforce sucessos e proponha novo desafio levemente superior.
- Por exemplo: professor demonstra agrupamento por dez com poucos objetos, pede que a aluna repita em grupos maiores e ensine a um colega.
Avaliação formativa no construtivismo: observar o processo e registrar progressos
De antemão, a avaliação formativa deve focalizar o processo, não apenas o produto final. Bem como, evidências sobre retorno efetivo estão compiladas em Avaliação formativa e feedback descritivo.
- O que observar: estratégias, justificativas, padrões de erro, persistência, interação e linguagem matemática.
- Ferramentas: planilhas de observação, portfólios com desenhos/fotos, rubricas simples, fichas de entrevista rápida.
- Frequência: observações diárias curtas e registros semanais mais sistemáticos. Use dados para ajustar objetivos e agrupamentos.
- Feedback: devolutiva positiva e orientadora para crianças e famílias; envolva familiares com sugestões de atividades em casa.
- Exemplos de itens para ficha: conta objetos até 10; agrupa objetos em pares; explica estratégia usada.
Em síntese, quando houver sinais de desafio persistente, considere encaminhamentos e estratégias específicas para dificuldades de aprendizagem na infância ou para crianças com dificuldades de comportamento.
Dicas práticas para planejar aulas com materiais manipulativos e jogos
Em primeiro lugar, planejar aulas construtivistas exige intencionalidade, flexibilidade e documentação.
- Plano rápido em 8 passos: identificar objetivo observável; escolher material; preparar situação-problema; definir tempos (exploração, socialização, registro); elaborar perguntas norteadoras; preparar variações; planejar registro de evidências; pensar devolutiva.
- Checklist pré-aula: materiais agrupados e etiquetados; espaço organizado; fichas de observação prontas.
- Sugestões de condução: começo com desafio curto; tempo de exploração individual antes do trabalho em pares; roda de socialização.
- Perguntas poderosas: “O que você está descobrindo agora?”, “Como verificou sua resposta?”, “Que outra maneira poderíamos usar?”
- Atividades de fechamento: registro coletivo no quadro; pequena tarefa para casa que reforce a ideia central.
- Planejamento para inclusão: versões simplificadas, recursos visuais e táteis (considere práticas inclusivas na educação básica).
- Sugestão de tempo por sequência: 5–10 min motivação; 15–25 min exploração; 10–15 min socialização; 5 min registro.
Conclusão
De maneira geral, você viu como a abordagem construtivista transforma a aprendizagem: não é decorar, é construir sentido. Assim, quando você coloca materiais manipulativos nas mãos das crianças, cria uma ponte entre o concreto e o abstrato. Logo, isso acende a curiosidade, gera perguntas reais e por fim, transforma o professor em mediador — desse modo, observando, fazendo perguntas e ajustando o desafio dentro da ZDP.
Em outras palavras, rotinas claras, centros de exploração e jogos bem planejados tornam a sala um laboratório vivo. Igualmente, erro vira pista. Do mesmo modo, registro e avaliação formativa viram bússola para suas próximas decisões. Em suma: plante sementes com atividades concretas e colha compreensão duradoura.
Por fim, caso queira continuar explorando, leia mais artigos e ideias práticas em formação continuada de professores.
Perguntas frequentes
1. O que é a corrente pedagógica construtivista para crianças aprender matemática?
É uma forma de ensino por ação: a criança descobre e constrói sentido com materiais e perguntas, mediada pelo professor.
2. Como você organiza uma aula construtivista de matemática para crianças?
Crie estações curtas, ofereça um desafio por vez, observe, faça perguntas e ajuste o nível.
3. Devo usar jogos manipulativos na sala para reforçar conceitos?
Dê peças, regras simples e objetivos rápidos; peça que a criança explique; você guia, não resolve.
4. Quais sinais mostram que seu aluno está entendendo a matemática concreta?
Ele explica com as mãos, resolve sem copiar e faz conexões entre jogos e problemas reais.
5. Como aplicar a Corrente pedagógica construtivista para ensinar crianças matemática concreta com jogos manipulativos na sala de aula?
Monte atividades práticas e rotativas, varie materiais e perguntas, incentive a troca entre pares e avalie pelo processo, não só pela resposta.
Publicar comentário